2022. 11. 1. 01:04ㆍ알고리즘
문제
여행을 떠난 세준이는 지도를 하나 구하였다. 이 지도는 아래 그림과 같이 직사각형 모양이며 여러 칸으로 나뉘어져 있다. 한 칸은 한 지점을 나타내는데 각 칸에는 그 지점의 높이가 쓰여 있으며, 각 지점 사이의 이동은 지도에서 상하좌우 이웃한 곳끼리만 가능하다.
현재 제일 왼쪽 위 칸이 나타내는 지점에 있는 세준이는 제일 오른쪽 아래 칸이 나타내는 지점으로 가려고 한다. 그런데 가능한 힘을 적게 들이고 싶어 항상 높이가 더 낮은 지점으로만 이동하여 목표 지점까지 가고자 한다. 위와 같은 지도에서는 다음과 같은 세 가지 경로가 가능하다.
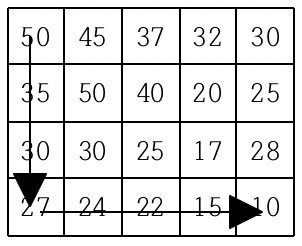
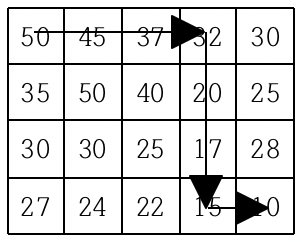
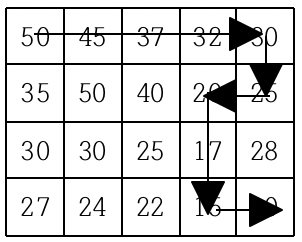
지도가 주어질 때 이와 같이 제일 왼쪽 위 지점에서 출발하여 제일 오른쪽 아래 지점까지 항상 내리막길로만 이동하는 경로의 개수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에는 지도의 세로의 크기 M과 가로의 크기 N이 빈칸을 사이에 두고 주어진다. 이어 다음 M개 줄에 걸쳐 한 줄에 N개씩 위에서부터 차례로 각 지점의 높이가 빈 칸을 사이에 두고 주어진다. M과 N은 각각 500이하의 자연수이고, 각 지점의 높이는 10000이하의 자연수이다.
출력
첫째 줄에 이동 가능한 경로의 수 H를 출력한다. 모든 입력에 대하여 H는 10억 이하의 음이 아닌 정수이다.
예제 입력 1
4 5
50 45 37 32 30
35 50 40 20 25
30 30 25 17 28
27 24 22 15 10
예제 출력 1
3https://www.acmicpc.net/problem/1520
1520번: 내리막 길
여행을 떠난 세준이는 지도를 하나 구하였다. 이 지도는 아래 그림과 같이 직사각형 모양이며 여러 칸으로 나뉘어져 있다. 한 칸은 한 지점을 나타내는데 각 칸에는 그 지점의 높이가 쓰여 있으
www.acmicpc.net
맛보기로 (1,1)에서 (n,m)까지 도달할 수 있는 dfs를 작성했는데 역시나 시간초과가 발생한다.
만약 (3,3)에서 (n,m)까지 도달할 수 있는 방법을 구해 3이라는 값을 얻었다면
(1,1)에서 어찌어찌하다 (3,3)에 도달한다면 (n,m)까지의 경로를 중복으로 탐색할 필요 없이 이전에 저장한 3이라는 값을 사용하면 된다.
따라서 dfs랑 메모이제이션이 필요한 dp를 같이 사용하는 문제라고 할 수 있겠다.
dp[i][j] = (i, j)에서부터 종점으로 갈 수 있는 경우의 수를 저장한다.따라서 우리는 시작점 dp[1][1]을 출력하면 정답이 나오게끔 해야한다.
dp[i][j]의 값들을 처음에 -1로 초기화해서, dp[i][j]가 -1이라면 메모이제이션을 위해 dfs 탐색을 실시하고,
-1이 아니라면 저장된 dp[i][j]의 값을 그대로 반환하면 된다.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Main {
static int n, m;
static int[][] map;
static int[][] dp;
static int[] dx = {1, 0, -1, 0};
static int[] dy = {0, 1, 0, -1};
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken());
m = Integer.parseInt(st.nextToken());
map = new int[n + 1][m + 1];
dp = new int[n + 1][m + 1];
for (int i = 1; i <= n; i++) {
Arrays.fill(dp[i], -1);
}
for (int i = 1; i <= n; i++) {
st = new StringTokenizer(br.readLine());
for (int j = 1; j <= m; j++) {
map[i][j] = Integer.parseInt(st.nextToken());
}
}
System.out.println(dfs(new Point(1, 1)));
}
private static int dfs(Point point) {
// 이미 저장된 dp값이 있다면 바로 반환한다.
if (dp[point.x][point.y] != -1) {
return dp[point.x][point.y];
}
if (point.x == n && point.y == m) {
return 1;
}
// 탐색을 하는 경우 -1에서 0으로 변경해준다.
dp[point.x][point.y] = 0;
for (int i = 0; i < 4; i++) {
int nx = point.x + dx[i];
int ny = point.y + dy[i];
if (nx < 1 || ny < 1 || nx > n || ny > m) {
continue;
}
if (map[nx][ny] < map[point.x][point.y]) {
dp[point.x][point.y] += dfs(new Point(nx, ny));
}
}
return dp[point.x][point.y];
}
static class Point{
int x;
int y;
public Point(int x, int y) {
this.x = x;
this.y = y;
}
}
}'알고리즘' 카테고리의 다른 글
| 프로그래머스: 파괴되지 않은 건물(lv2) [Java] - 포포 (0) | 2023.01.07 |
|---|---|
| 백준 1890: 점프 (0) | 2022.11.03 |
| 백준 2206: 벽 부수고 이동하기 [Java] - 포포 (0) | 2022.10.07 |
| 프로그래머스: 더 맵게(lv2) [Java] (0) | 2022.08.30 |
| 프로그래머스: 뉴스 클러스터링(lv2) [Java] (0) | 2022.08.17 |